This page is the second of three in a series about clock domains.
Scope
As already mentioned in the previous page, if a path goes across clock domains of related clocks, no special treatment is required by the logic. Nevertheless, it's required to make sure that the FPGA tools enforce the timing constraints on this path, in order to guarantee the timing requirements of the synchronous element at the destination (setup and hold). So this case is handled as if there was no clock domain crossing at all, in the sense that the path is timed.
However if the clocks are unrelated clocks, resynchronization logic is required: There must be code in Verilog (or some other language) that is dedicated to solve this issue. This page goes through the basics of how to do this.
Use a FIFO if you can
I thought it would be just fair to begin with how to avoid this headache altogether, in favor of those who have the possibility to escape. Which is:
Dual-clock FIFOs, which are generated by the FPGA tools, are definitely the safest way to go across clock domains. This is the most common solution, and the fact that this method is so widely used is by itself a reason to trust it.
In particular, if you're new with FPGAs, there's a good reason to prefer a FIFO, even if you'll need to change your own design a bit for that purpose. Using a FIFO might consume slightly more resources than logic that is tailored for your purpose. Note however that a block RAM is usually not required if the FIFO's depth is shallow. So the difference isn't necessarily worth the risk of messing up.
Often the FIFO is the natural solution for going across clock domains, in particular when there's a data stream from one functional unit to another. But even when it's not all that natural, it's often possible to reorganize the logic to make things fit. For example, if logic in one clock domain needs to notify logic in another clock domain about some event, this can be done by encoding a message word and write it into a shallow FIFO. A solution of this sort isn't only less prone to bugs, but it's also likely to result in a more organized and readable design.
How to connect and use FIFOs is discussed extensively in this series of pages.
Resynchronization logic for a single bit
If a FIFO doesn't solve your problem, it's time to roll up our sleeves and implement the resynchronization logic for a safe clock domain crossing. The rest of this page is limited to going across clock domains with a signal that has the width of a single bit. This is the cornerstone for any resynchronization logic, and there's plenty to say about this seemingly simple case.
The next page in this series discusses how to go across clock domains with wider signals, based upon the metastability guard technique that is presented below.
Metastability
Before moving on to solutions, it's important to understand what happens when the timing requirements of a flip-flop are violated. In other words, when the signal at its data input isn't stable at the time period that starts tsu before the clock edge, and ends thold after it. The relevant clock edge is of course the one at the flip-flop's clock input. It's this clock edge that causes it to sample the data input.
Clearly, if the data changes during this time period, the output of the flip-flop after this clock edge is unpredictable. But it's even worse than so: It may take the flip-flop significantly longer than usual to present a legal '0' or '1' at the flip-flop's output. Even though the flip-flop is designed to keep the output stable on one of these two possible values (i.e. '0' or '1'), a violation of the timing requirements can make the flip-flop stay in an unstable condition for a short while. Or, to use the official term, the flip-flop is metastable.
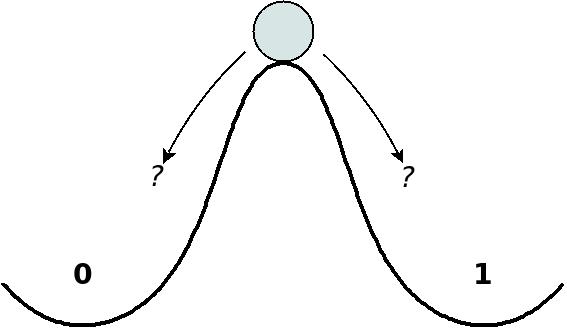
I won't skip the cliché image with the ball standing at the tip of a hill, which is often used to depict the unstable situation that the flip-flop can reach:
Metastability is a much bigger issue than just the uncertainty of what the flip-flop eventually lands on. This is true in particular if the flip-flop's output is connected to more than one destination: Because it takes a longer time to land on either a '0' or '1', the signal might become stable too late for the flip-flops at the destination. As a result, some flip-flops at the destinations may receive the wobbling signal as '0' and other flip-flops may receive it as '1'. This mismatch can bring the logic into an illegal state, and from this situation the logic can behave in black magic style. So a flip-flop that is at risk for metastability should never be connected to more than one logic element.
To tackle metastability, it would have been nice to know how long it takes for the flip-flop to fall into one of its stable states. Unfortunately, there's no definite answer to that. It's exactly like asking how long the ball will stay at the top of a hill: It depends on a lot of factors, and odds are that random vibrations will eventually make it fall down this way or the other. Same with a flip-flop's metastability: It will be brought out of this state by virtue of random noise in the electronic circuits, or whatever else.
So in theory, a flip-flop can remain in the condition of metastability forever, but in reality it will fall into one of its stable states after a short while. The time it stays in this condition is a random variable. And plenty of experiments and simulations have been made in the attempt to estimate the behavior of this random variable. However none of these attempts is really relevant, since the behavior depends on the manufacturing technique of the silicon, temperature, the noise level from crosstalk and whatnot.
So once again, even though it would have been convenient to have a specified maximal time that the flip-flop will never exceed in the state of metastability, there is no such limit. It's not even possible to obtain an approximate figure, because newer manufacturing processes make flip-flops that tend to leave the state of metastability sooner.
Instead, this is the idea to get used to: When you go across clock domains with unrelated clocks, there's always a chance that some flip-flop will remain in the state of metastability longer that the design can tolerate, and something will go wrong as a result of that. The only thing we can do as designers is to reduce this risk. We can, at best, achieve an MTBF (Mean Time Between Failure) that one can live with.
Luckily, there's a well-established technique to achieve exactly that, which brings us to the next topic.
The metastability guard
To make a long story short, let's revisit the first code example from the previous page. If @clk1 and @clk2 are unrelated clocks, the common resynchronization logic for obtaining a stable @bar from @foo is
reg foo, bar, bar_metaguard;
always @(posedge clk1)
foo <= !foo;
always @(posedge clk2)
begin
bar_metaguard <= foo;
bar <= bar_metaguard;
end
As its name implies, @bar_metaguard is a metastability guard. The timing requirements of the flip-flop that implements @bar_metaguard are occasionally violated while sampling @foo. Hence @bar_metaguard can have short moments of metastability. Because this flip-flop is expected to recover from this state quickly, it will be stable quickly enough to meet @bar's setup timing requirement. Accordingly, @bar can be used reliably inside @clk2's clock domain.
This explanation may sound inaccurate, and it's indeed so. It actually contradicts what I wrote about metastability above, because there is no failsafe solution to metastability. I'll come back to that further below. But for now, let's stick to the common practice, which is to add the metastability guard as shown above, and not worry about it anymore. And truth to be told, I've never heard about someone having problems with this.
Those who want to be extra safe, add more registers. So a double metastability guard is done something like this:
reg foo, bar, bar_metaguard_a, bar_metaguard_b;
always @(posedge clk1)
foo <= !foo;
always @(posedge clk2)
begin
bar_metaguard_a <= foo;
bar_metaguard_b <= bar_metaguard_a;
bar <= bar_metaguard_b;
end
@bar_metaguard_a is the first metastability guard. If we're unlucky, it remains in the metastability state for too long, and @bar_metaguard_b's timing requirements are violated. Consequently, @bar_metaguard_b has a period of metastability on the next clock cycle. But this time the period of metastability is brief, one can hope: Lightning never strikes in one place twice, they say. But of course @bar_metaguard_b can also remain in the metastability state long enough to violate @bar's timing. But what is the probability for that? Remember that the goal is to obtain a reasonable MTBF.
To summarize: If you're looking for the cookbook solution on how to go across a clock domain with a single bit, this is it. One metastability guard or two metastability guards will do the job nicely. If you're looking for a solution that never fails, unfortunately this is impossible. But if you want to reduce the probability for mishaps to the extent possible, read on.
Timing analysis of metastability
So now let's go back to the example above with a single metastability guard, and ask why I was so sure that @bar_metaguard recovers from metastability quickly enough. The answer, as already mentioned, is that there's no reason to be sure.
Nevertheless, let's make a bit of a timing analysis. Both @bar_metaguard and @bar are synchronous with the same clock. Assuming that no special timing constraints have been assigned to these registers specifically, the path between them will be limited by @clk2's timing constraint (clock period). In other words, the tools ensure that in the absence of metastability, the input signal of @bar is sampled with legal timing.
But the whole point with @bar_metaguard was that it's allowed metastability occasionally. So the timing analysis is insufficient: In reality, the time that the flip-flop spends in the metastability state is an addition to its clock-to-output time. In other words, metastability means that the output of the flip-flop becomes stable later than its usual delay. So if the path between @bar_metaguard and @bar has a slack that is nearly zero (i.e. its propagation delay is good enough to achieve timing, but not with a margin), metastability may bring the path's total delay above the allowed limit. Such event would cause a timing violation on @bar's input. Of course this applies to the worst case in temperature, voltages and manufacturing process, and yet: The fact that the tools apply the regular timing constraint on the metastability guard's output means that it doesn't ensure the necessary timing requirements.
Luckily, this is easy to fix. Or improve, I should say. The method is to add a tighter timing constraint on all paths from metastability guards to the registers that need to be reliable. In other words, the idea is to allow less propagation delay on these paths. By reducing the time that is allowed for propagation delay, this time is given for the sake of recovering from metastability.
For example, if all metastability guard registers have the *_metaguard suffix, a single timing constraint can be written to require that all paths from them get some extra time for stabilizing. For Vivado, such constraint would say:
set_max_delay -from [ get_cells -hier -filter {name=~*_metaguard*} ] 0.75
(set_max_delay is explained on the page about timing exceptions)
This timing constraint means that any path that starts at a metastability guard has 0.75 ns to reach its destination (these paths are selected by the suffix of the registers' names). This is the minimum delay that I managed to obtain without failing the timing constraint on a specific FPGA that I tried this on (so it may be different on other FPGAs). The way to reach this number it is to pick a lower number until the tools fail to achieve this constraint. Upon this failure, increase this number as necessary to achieve a very small slack (e.g. 0.2 ns). This forces the tools to do their very best on these paths.
This set_max_delay command is equivalent to request a clock period of 0.75ns (1333 MHz). So if, for example, the actual clock period is 250 MHz (4 ns), achieving this timing constraint gives a surplus of at least 4 – 0.75 = 3.25 ns. Hence if the metastability guards are in metastability state for up to 3.25 ns, no timing violation will occur, thanks to this set_max_delay constraint.
This is of course better than no assurance at all, but is 3.25 ns enough? Is it much? Is it enough to ensure a virtually failsafe transition of clock domains?
As already said, the answer to this depends on several factors. Judging by experiments that have been published, my personal impression is that it's extremely unlikely to see a flip-flop remain in the metastability state for as long as 1 ns, on any FPGA that is practically used today. But it's difficult to say anything for sure on this matter.
But by adding this timing constraint, and hence pushing the tools to do their best, you put your FPGA design in line or better than everyone else's situation. So in the spirit of Golden Rule #4 (don't push your luck), put yourself in a position that if it fails for you, a whole lot of other people will have a reason to complain as well.
Another insight from this discussion on timing is that if the clock's frequency is high in terms of the FPGA that is used, a double metastability guard might be a good idea. This is true in particular if the extra timing constraint that was suggested above isn't used: As mentioned above, metastability consumes the path's slack. As the clock period becomes smaller (the frequency becomes higher), there is often less slack, and hence less extra time for metastability.
Finally, let's ask how come virtually everyone ignores this whole issue about timing, and yet nobody complains about problems. I'll offer a few possible explanations, but these are just speculations.
So the first explanation is that there's a good chance that the tools place the metastability guard very close physically on the FPGA's logic fabric to the other flip-flop. Hence the propagation delay between these two flip-flops (e.g. @bar_metaguard to @bar) is very short in terms of that FPGA anyhow. This tight placement is however not ensured without explicit timing constraints, as discussed above.
Inside the official FIFOs that are provided by the FPGA's vendors, pairs of flip-flops of this sort are often found on the same slice. Regardless, official FIFOs can be trusted to have this issue sorted out.
Another thing is that as FPGAs become faster, and higher clock frequencies become possible, it turns out that the flip-flops also get out of metastability quicker. So the time it takes to recover from metastability plus the propagation delay, still remains significantly shorter than the clock period of the clock.
So it's no surprise that most people just add the metastability guard and don't worry about it anymore. That's however not an excuse for being lazy about adding a constraint.
Limitations on the clocks' frequencies
I haven't said much so far about the frequencies of the clocks in either clock domain. For example, what happens if the clock in the source's clock domain (@clk1) is faster than the destination's clock (@clk2)?
Because no synchronization is required between the clocks, it doesn't matter if the source's frequency is higher or lower per se. But if the source's signal (@foo) changes too fast, it might change back and forth before the flip-flop at the destination had a chance to sample this change. So if all transitions must be visible at the destination, the clock period of the source must be slightly longer (i.e. have a lower frequency) than the destination's clock.
How much longer? Not by very much. Or if you insist on an accurate answer: That depends primarily on the timing requirements of the flip-flop at the destination. Here's a quick calculation (skip this unless it really interests you):
If this flip-flop's input changes exactly tsu before that flip-flop's clock edge, it's on the edge of being sampled properly, so it must be sampled on the next clock cycle. Otherwise, maybe this change was missed. To sample this change on the next clock cycle reliably, the input signal must remain steady until thold after the next clock edge. So the source's clock period must be longer than the destination's clock period by tsu + thold + 2tj. tj is the uncertainty in the clock period (jitter). The jitter is counted twice, once for the source's clock and the second time for the destination's clock.
So tsu + thold + 2tj is what I meant with "slightly longer" clock period for the source's clock.
Telling the tools about the metastability guards
The documentation of some FPGA tools recommends to add an attribute to flip-flops that are used as metastability guards. This prevents the tools from making manipulations on these flip-flops. It also encourages the tools to put the metastability guard on the same slice as the next flip-flop, so the routing is as short as possible.
For example, Vivado has an attribute with the name ASYNC_REG. So as before, if all metastability guard registers have the *_metaguard suffix, this row in the XDC file sets the attribute as necessary:
set_property ASYNC_REG true [get_cells -hier -filter {name=~*_metaguard*}]
It's also possible to set this attribute inside the Verilog code.
However, this attribute is unlikely to make any difference, because the tools usually handle metastability guards correctly anyhow.
This concludes the second page in this series. The next page shows techniques for passing data across clock domains.