Linear-Feedback Shift Register의 Galois 와 Fibonacci 다항식 간의 변환

소개

이 페이지는 한 문장으로 요약할 수 있습니다. LFSR의 다항식을 Galois 형식에서 Fibonacci 형식으로 변환하려면 계수의 순서를 반대로 하십시오.

예를 들어 scramblers에서 자주 사용되는 LFSR 용 도면은 다음과 같습니다.

D 로 표시된 각 블록은 하나의 clock cycle의 delay 입니다. 이 LFSR를 Galois 다항식으로 표현하면 다음과 같습니다.

G(x) = x¹⁶ + x⁵ + x⁴ + x³ + 1

다항식의 지수(3, 4, 5)는 각 XOR의 왼쪽에 있는 delay elements 의 수를 나타냅니다.

이 그림과 같이 동일한 LFSR를 Fibonacci 형식으로 구현할 수 있습니다.

이 두 도면 사이의 유사성에도 불구하고 화살표의 방향은 반대입니다. LFSRs 의 구현은 완전히 다릅니다.

Fibonacci 다항식(또는 feedback 다항식)은 다음과 같습니다.

F(x) = x¹⁶ + x¹³ + x¹² + x¹¹ + 1

다항식의 차수는 n=16이 므로 G(x) 의 각 xⁱ는 F(x) 에서 x^n-i로 표시됩니다. 이 페이지의 나머지 부분에서는 이것이 우연이 아닌 이유를 보여줍니다.

LFSRs에 대한 일반적인 설명은 이 주제에 대한 Wikipedia 페이지를 참조하십시오.

LFSR 및 digital filters

digital filters 의 이론(예: FIRs 및 IIRs)은 일반적으로 field of complex numbers에 적용됩니다. 그러나 이 이론을 GF(2) 에 적용하는 것도 가능합니다. 즉, 두 개의 숫자로 구성된 finite field (Galois Field)입니다. 0 및 1. 참고할 사항이 몇 가지 있습니다.

• 이 field 의 plus operator는 XOR와 동일합니다.
• 모든 곱셈에는 정수만 포함됩니다. 사실 짝수로 곱하는 것은 0으로 곱하는 것과 같습니다. 마찬가지로 홀수로 곱하는 것은 1로 곱하는 것과 같습니다. 이 숫자가 양수인지 음수인지는 중요하지 않습니다.
• 곱셈이 있는 이 규칙 때문에 plus 와 minus는 같은 의미입니다. 둘 다 ⊕ ( XOR을 의미)로 교체할 수 있습니다.

digital filters 의 기본 이론은 시스템이 Linear time-invariant (LTI)인 것만을 요구합니다. LFSR는 XOR이 선형이고 LFSR의 동작이 시불변이기 때문에 이러한 요구 사항을 충족합니다.

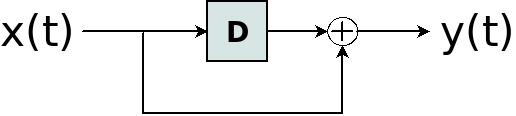
가장 흥미로운 결과는 z-transform을 사용하여 LFSRs를 분석할 수 있다는 것입니다. 예를 들어 다음 그림을 고려하십시오.

이는 다음 방정식으로 설명할 수 있습니다.

y(t) = x(t) ⊕ x(t-1)

t는 시간을 나타내는 정수입니다.

이것을 FIR로 취급하고 이 방정식의 z-transform을 작성할 수 있습니다.

Y(z) = X(z) + X(z)z^-1=X(z) (1 + z^-1)

따라서 "impulse response"는 평소와 같이 정의할 수 있습니다. H(z) = Y(z)/X(z)또는 간단히:

H(z) = 1 + z^-1

하지만 이 필터 두 개를 차례로 넣으면 어떻게 될까요? 이 필터의 "impulse response"는 무엇입니까?

digital filters 에 대한 이론에는 간단한 대답이 있습니다.

H₂(z) = H(z)H(z) = (1 + z^-1)(1 + z^-1) = 1 + 2z^-1 + z^-2

GF(2)에서 짝수의 곱셈은 0의 곱셈과 같습니다. 따라서,

H₂(z) = 1 + 2z^-1 + z^-2 = 1 + 0z^-1 + z^-2=1 + z^-2

이는 이에 해당합니다.

마지막 두 그림에 표시된 필터가 동일하다고 보기는 쉽지 않습니다. 그러나 두 필터 모두 동일한 x(t)를 공급할 때 동일한 y(t)를 생성합니다. 따라서 두 번째 delay element 에 저장된 값이 동일하지 않더라도 필터는 동일합니다.

이 예는 z-transform (및 다항식과 유사한 기술)를 사용하여 logic filters를 분석하는 이점을 보여줍니다.

z^-1대신 기호 D 또는 D^-1이 자주 사용된다는 점을 언급해야 합니다. 사실 Galois 와 Fibonacci 다항식에서 x를 사용하는 것은 z^-1와 같은 의미를 갖는다. 이 모든 기호는 delay을 의미합니다.

Galois LFSR

Fibonacci 표현을 찾기 위해 Galois LFSR부터 살펴보겠습니다.

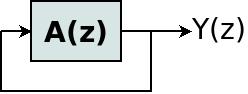
위의 Galois LFSR 도면을 고려하십시오. delay lines 및 taps 의 행은 FIR 필터로 볼 수 있으며 A(z)로 표시합니다. 따라서 Galois LFSR는 다음과 같습니다.

feedback로 인해 Y(z) 의 방정식은 다음과 같습니다.

Y(z) = Y(z)A(z)

그렇다면 이 FIR의 매개변수와 Galois 다항식 사이의 연결은 무엇입니까? Galois 다항식의 일반 형식을 작성해 보겠습니다.

G(x) = xⁿ + g_n-1x^n-1+ g_n-2x^n-2+…+ g₀

아래 수학을 단순화하기 위해 g_n은 이 표현식에 나타나지 않습니다. 게다가 g_n은 항상 1와 같습니다.

G(x) 와 A(z) 의 관계는 다음과 같습니다.

A(z) = g_n-1z^-1+g_n-2z^-2+…+g₁z^1-n+g₀z^-n

이것이 올바른 이유는 무엇입니까? 위 그림에서 Galois LFSR를 가져와 이 표현이 어떻게 작동하는지 보여드리겠습니다.

먼저 g₅에 해당하는 XOR을 살펴보자. 숫자 5는 이 XOR의 왼쪽 에 5개의 delay elements가 있다는 것을 의미합니다. 그러나 z 의 지수는 XOR 와 FIR의 output사이에 있는 delay elements 의 개수에 따라 달라집니다. XOR오른쪽 에 있는 delay elements 입니다. 총 16개의 delay elements가 있습니다. 따라서 g₅는 A(z) 에서 g₅z^-11로 나타납니다. 이는 g_n-iz^-i 패턴과 일치합니다.

이것을 설명하는 또 다른 방법은 A(z)를 time domain에서 FIR 로 보는 것입니다. 이 FIR의 input은 x(t)가 고 output은 y(t)입니다.

y(t) = x(t–16) ⊕ x(t–13) ⊕ x(t–12) ⊕ x(t–11)

다시 한 번, t는 시간을 나타내는 정수입니다. 이 표현은 feedback이 없는 Galois LFSR를 나타냅니다. 이 FIR의 transfer function은 다음과 같습니다.

A(z) = Y(z)/X(z) = z^-16 + z^-13 + z^-12 + z^-11

이것은 G(x) = x¹⁶ + x⁵ + x⁴ + x³ + 1이 있는 A(z) 에 대한 일반적인 표현과 일치합니다.

Fibonacci 동급

Fibonacci 형식의 LFSR는 다음 다항식으로 표현됩니다.

F(x) = f_nxⁿ+f_n-1x^n-1+…+f₁x + 1

f₀은 항상 1와 같기 때문에 이 다항식에 나타나지 않습니다. 이는 G(x)에서 g_n이 나타나지 않는 것과 유사합니다.

이 다항식의 구현은 다음과 같습니다.

y(t) = f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n)

따라서 z transform은 다음과 같습니다.

Y(z) = f₁Y(z)z^-1+f₂Y(z)z^-2+…+f_nY(z)z^-n

B(z)를 다음과 같이 정의해 보겠습니다.

B(z) = f₁z^-1+f₂z^-2+…+f_nz^-n

따라서Y(z)는 다음과 같이 작성할 수 있습니다.

Y(z) = Y(z)B(z)

위에서 Y(z) = Y(z)A(z)를 떠올려 보십시오. 따라서 LFSR 의 Fibonacci 형태가 Galois 다항식에 의해 주어진 LFSR 와 동일하게 동작한다면 A(z) = B(z)를 따른다. 이는 또한 다음을 의미합니다.

f_i=g_n-i (i=1,2, … , n)

그래서 제가 처음부터 말했듯이: LFSR의 다항식을 Galois 형식에서 Fibonacci 형식으로 변환하려면 계수의 순서를 반대로 하십시오.

LFSR의 inverse filter

다시 한 번 이것은 LFSR의 Fibonacci 구현입니다.

y(t) = f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n)

하지만 이 표현은 다음과 같이 다시 쓸 수도 있습니다.

y(t) + f₁y(t-1) + f₂y(t-2) +…+ f_ny(t-n) = 0

( + 와 –는 GF(2)에서 동일합니다.)

따라서 Fibonacci 다항식의 계수는 항상 값 0을 얻기 위해 y(t-i) 의 값에 대해 XOR을 수행하는 방법도 알려줍니다. 즉, 이것은 흥미로운 FIR를 설명합니다.

마지막 표현의 z transform은 다음과 같습니다.

Y(z) + f₁Y(z)z^-1+f₂Y(z)z^-2+…+f_nY(z)z^-n = 0

또는 동등하게:

Y(z)(1+ f₁z^-1+f₂z^-2+…+f_nz^-n) = Y(z)H(z) = 0

Y(z)H(z)는 Y(z)에 필터 H(z)를 적용했을 때의 output 입니다. 그리고 이 output은 0입니다.

따라서 H(z)는 FIR filter의 transfer function 입니다. 이 FIR 에 F(x)로 정의된 LFSR 의 output을 공급하면 output은 항상 0이 됩니다. 위의 B(z) 정의에서 이 FIR의 transfer function은 다음과 같습니다.

H(z) = 1 + f₁z^-1+f₂z^-2+…+f_nz^-n

또는 time domain에서 input이 x(t)가 고 output이 y(t)인 경우:

y(t) = x(t) ⊕ f₁x(t-1) ⊕ f₂x(t-2) ⊕ … ⊕ f_nx(t-n)

x(t)가 F(x)로 정의된 LFSR 의 output이 면 y(t)는 모든 t에 대해 0입니다.